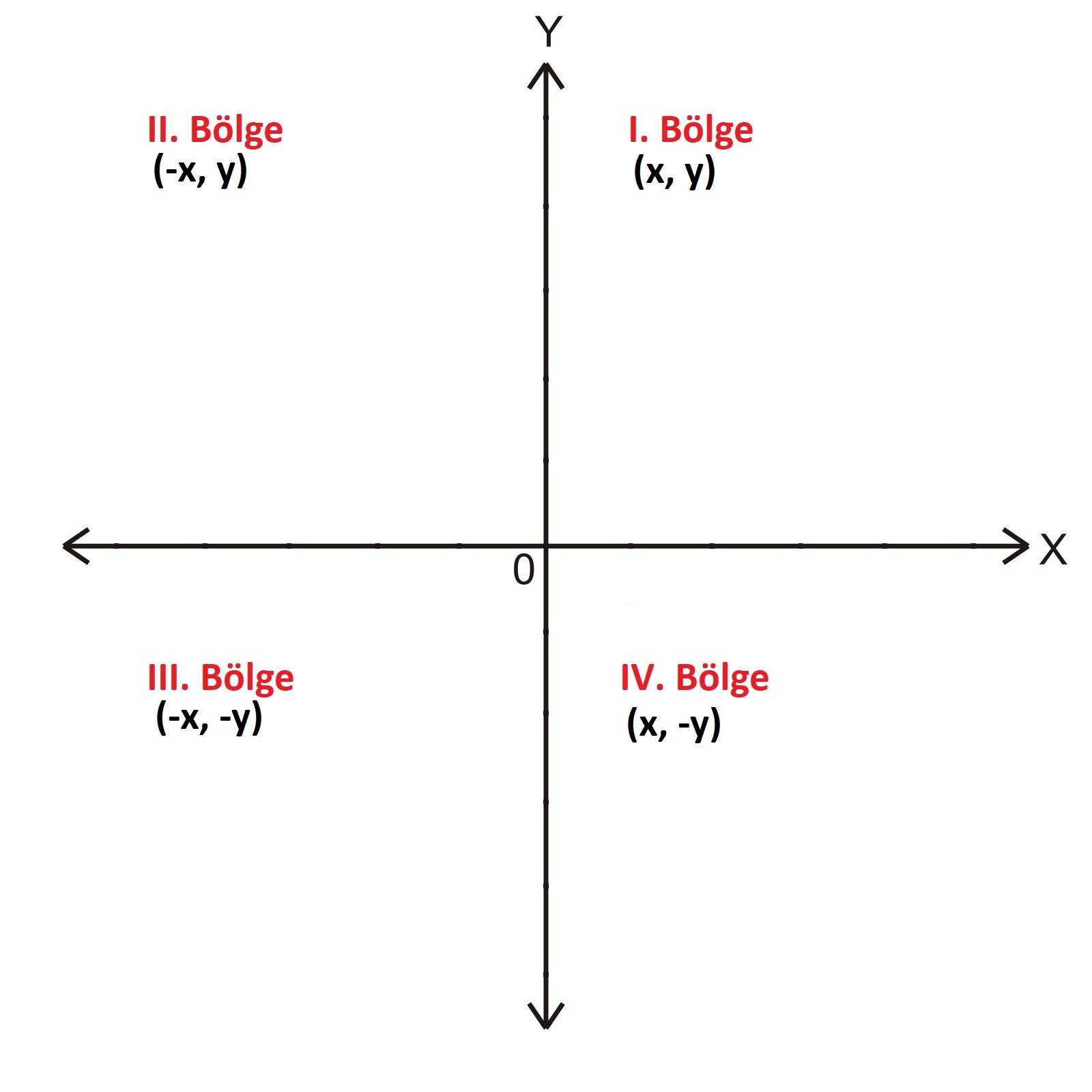
Analitik Düzlemde Bölgeler

Analitik Düzlemde x eksenine “apsis”, y eksenine “ordinat” denir.  Analitik düzlem üzerindeki apsis ve ordinatın pozitif ve negatif durumları;

I. Bölge: {(x, y) | x, y ∈ R  x > 0,  y > 0}
II. Bölge: {(x, y) | x, y ∈ R  x < 0,  y > 0} 
III. Bölge: {(x, y) | x, y ∈ R  x < 0,  y < 0} 
IV. Bölge: {(x, y) | x, y ∈ R  x > 0,  y < 0} 

 

İki Nokta Arasındaki Uzaklık:

İki Nokta Arasındaki Uzaklık
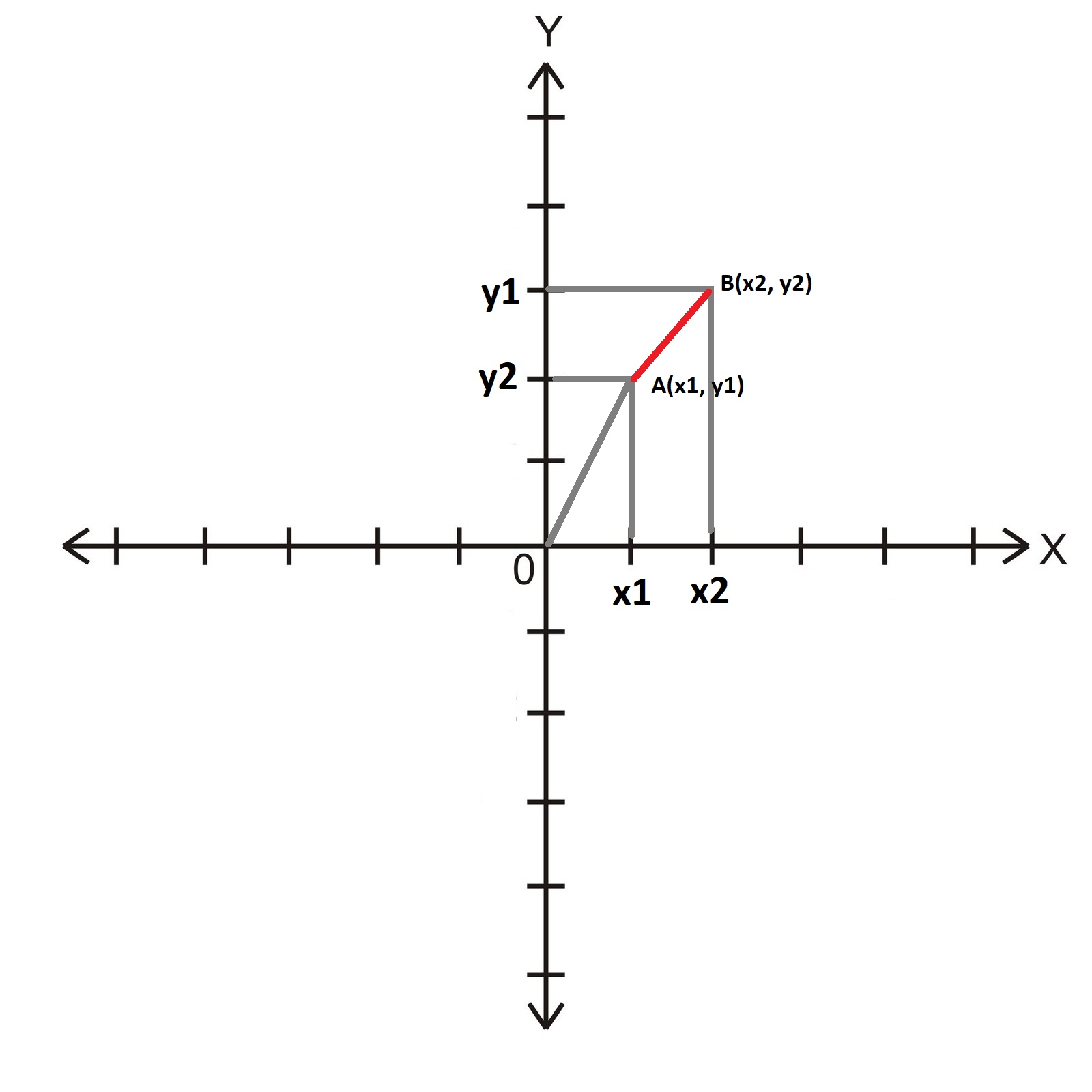
\color{white}{|AB| = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}}

\color{white}{|OA| = \sqrt{x^2_1 + y^2_1}}

 

Doğru Parçasının Orta Noktasının Koordinatları:

|AC| = |BC| ve  C(x0, y0)  olmak şartıyla;

\color{white}{x_0 = \frac{x_1+x_2}{2}}

\color{white}{y_0 = \frac{y_1+y_2}{2}}

 

Bir Doğru Parçasının Belirli Bir Oranda Bölen Noktanın Koordinatları:

Bir doğru parçasını belirli bir oranda bölen noktanın koordinatları

 

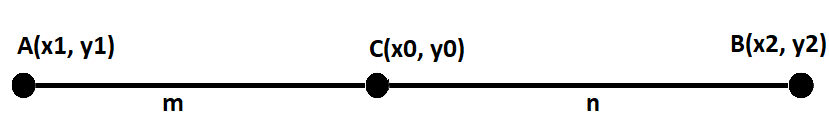
\color{white}{\frac{|CA|}{|CB|} = \frac{m}{n} = k}  olmak üzere;

\color{white}{x_0 = \frac{x_1 - kx_2}{1 - k}}

\color{white}{y_0 = \frac{y_1 - ky_2}{1 - k}}

 

Bir Noktanın Simetrileri:

A(x, y) noktasının;

1) x eksenine göre simetriği; (x, -y)‘dir.
2) y eksenine göre simetriği (-x, y)‘dir.
3) O(0, 0) noktasına (orijine) göre simetriği (-x, -y)‘dir.
4) I. açıortay (y = x) doğrusuna göre simetriği; (y, x)‘dir.
5) II. açıortay (y = – x) doğrusuna göre simetriği; (-y, -x)‘dir.
6) x = a doğrusuna göre simetriği; (2a-x, y)‘dir.
7) y = b doğrusuna göre simetriği; (x, 2b-y)‘dir.
8) B(a, b) noktasına göre simetriği (2a – x, 2b -y)‘dir.

 

Doğrunun Eğimi:

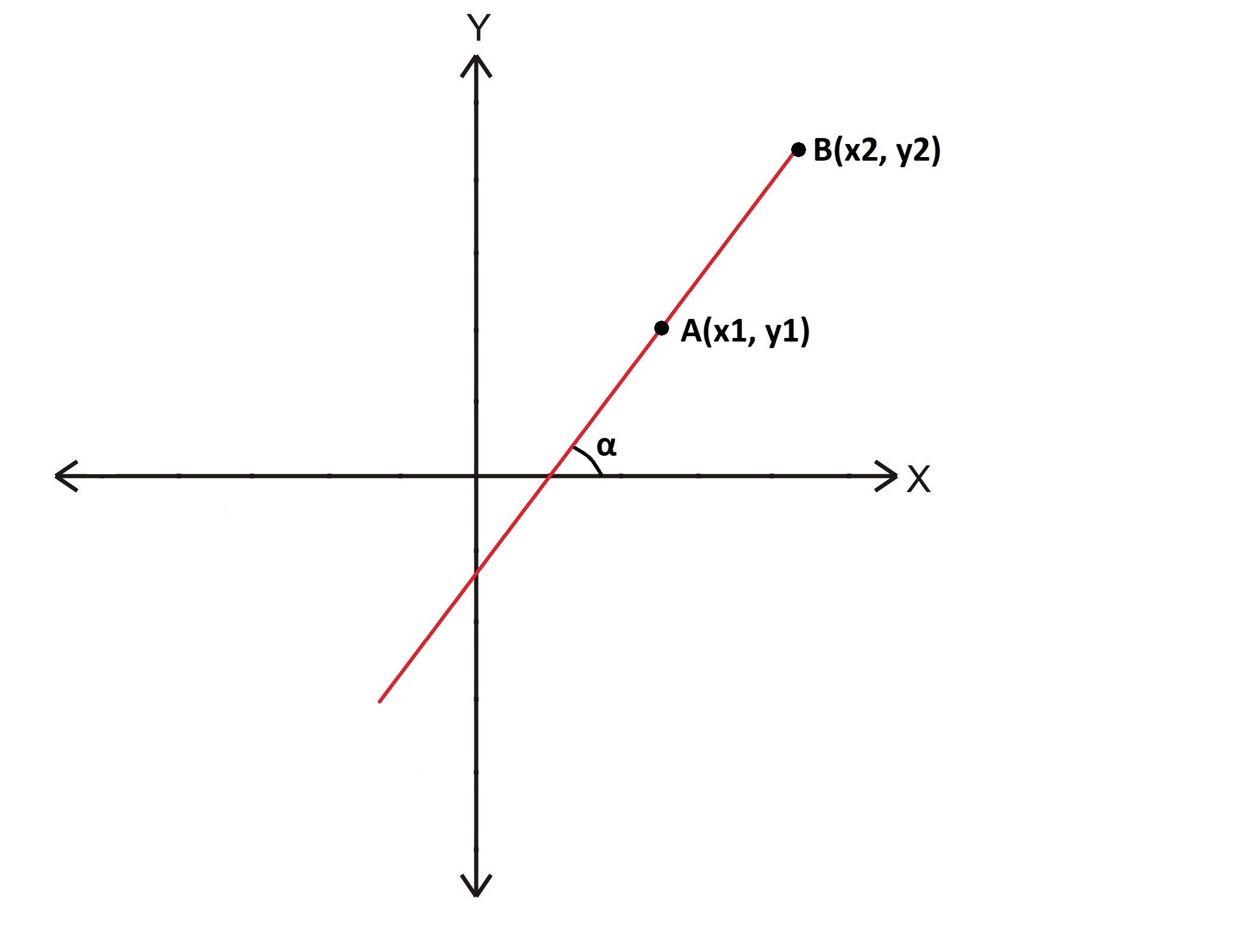
Doğrun eğimi

AB doğrusunun eğimi m olsun;

\color{white}{m = tan\alpha = \frac{y_1 - y_2}{x_1 - x_2}}

Burada dikkat edilirse, eğim doğrunun açısının tanjantına eşittir. Eğer tanjant pozitif bölgede ise, eğim pozitif; negatif bölgede ise, eğim negatiftir.

 

AB doğrusunun denklemi ax + by + c = 0 ise;

\color{white}{m = -\frac{a}{b}}

 

Ayrıca; fonksiyonun grafiğine teğet olan doğrunun eğimi, fonksiyonun birinci mertebeden türevine eşittir.

\color{white}{f'(x) = m_{teget}}

 

Fonksiyonun artan olduğu bölgede; f'(x) > 0, negatif olduğu bölgede ise; f'(x) < 0’dır.

\color{white}{f'(x).m_{normal} = -1}

\color{white}{m_{teget}.m_{normal} = -1}

 

Doğrunun Denklemi:

Eğimi m ve bir noktası A(x1, y1) olan doğrunun denklemi;

\color{white}{y - y_1 = m(x - x_1)}

 

İki noktası A(x1, y1) ve B(x2, y2) olan doğrunun denklemi;

\color{white}{\frac{y - y_1}{x - x_1} = \frac{y_1 - y_2}{x_1 - x_2}}

Eksenleri kestiği noktaları bilinen doğru denklemi;
Eksenleri kestiği bilinen doğru denklemi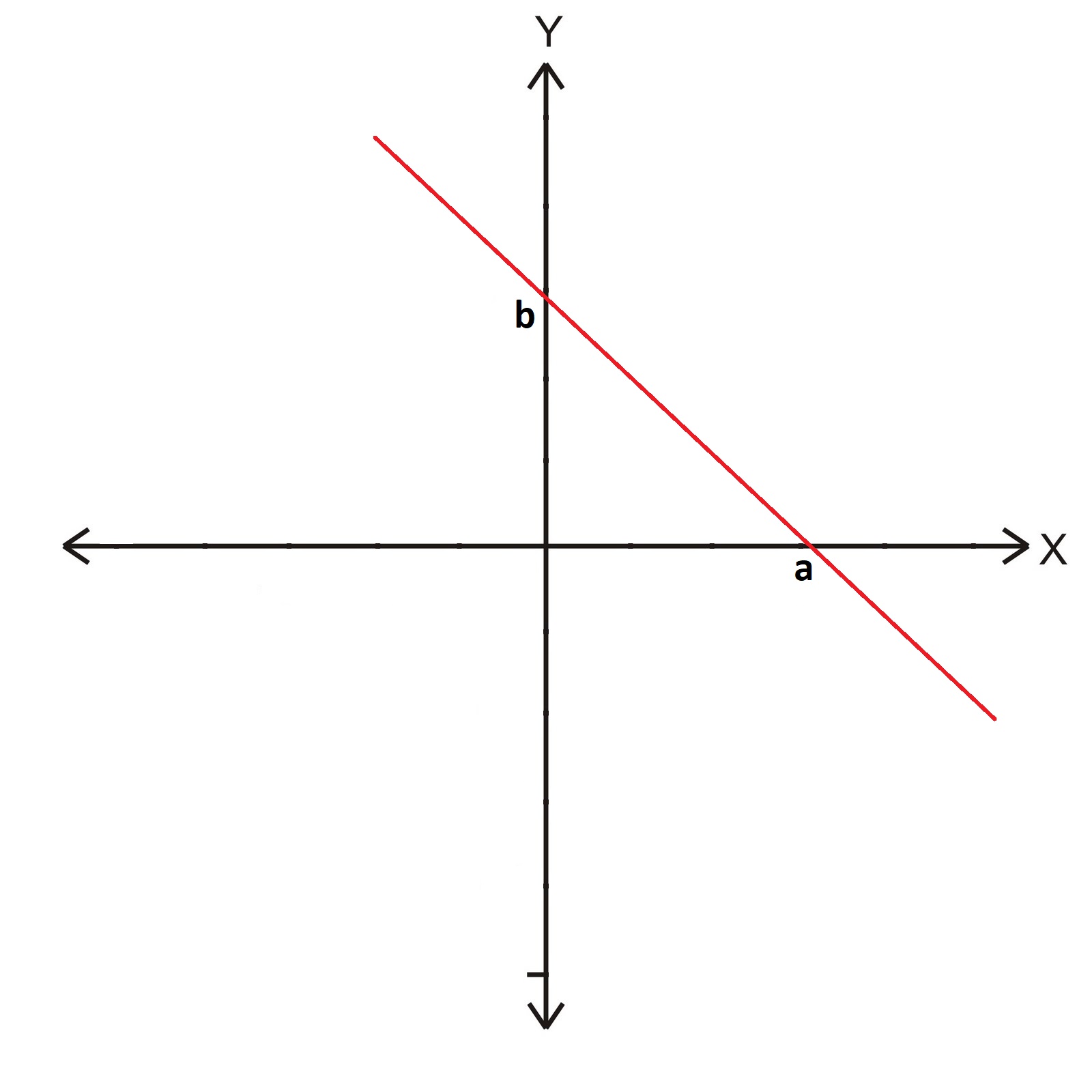

\color{white}{\frac{x}{a} = \frac{y}{b} = 1}

 

Bir Noktanın Bir Doğruya Olan Uzaklığı:

Bir noktanın bir doğruya olan uzaklığı

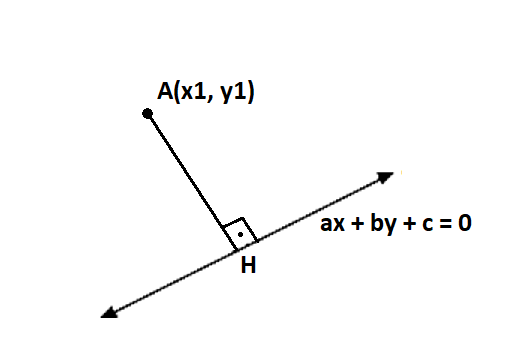
\color{white}{|AH| = \frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}}

 

İki Paralel Doğru Arasındaki Uzaklık:

Paralel iki doğru arasındaki uzaklık

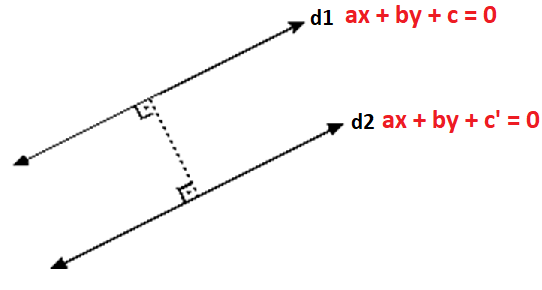
\color{white}{x = \frac{|c - c'|}{\sqrt{a^2 + b^2}}}

 

İki Doğrunun Birbirine Göre Durumları:

1) İki doğru birbirine paralel ise (d1 // d2); eğimleri birbirine eşittir.

\color{white}{d_1 // d_2 \ \to \ m_1 = m_2}

 


2) İki doğru birbirine dik ise (d1 ⊥ d2), eğimler çarpımı -1’dir.

\color{white}{d_1 \perp d_2 \ \to \ m_1.m_2 = -1}


3) İki doğru birbirine çakışmış / kesişmiş ise doğrular arasında ortak çözüm yapılır.

 

İki Doğru Arasındaki Açılar:

İki doğru arasındaki açılar

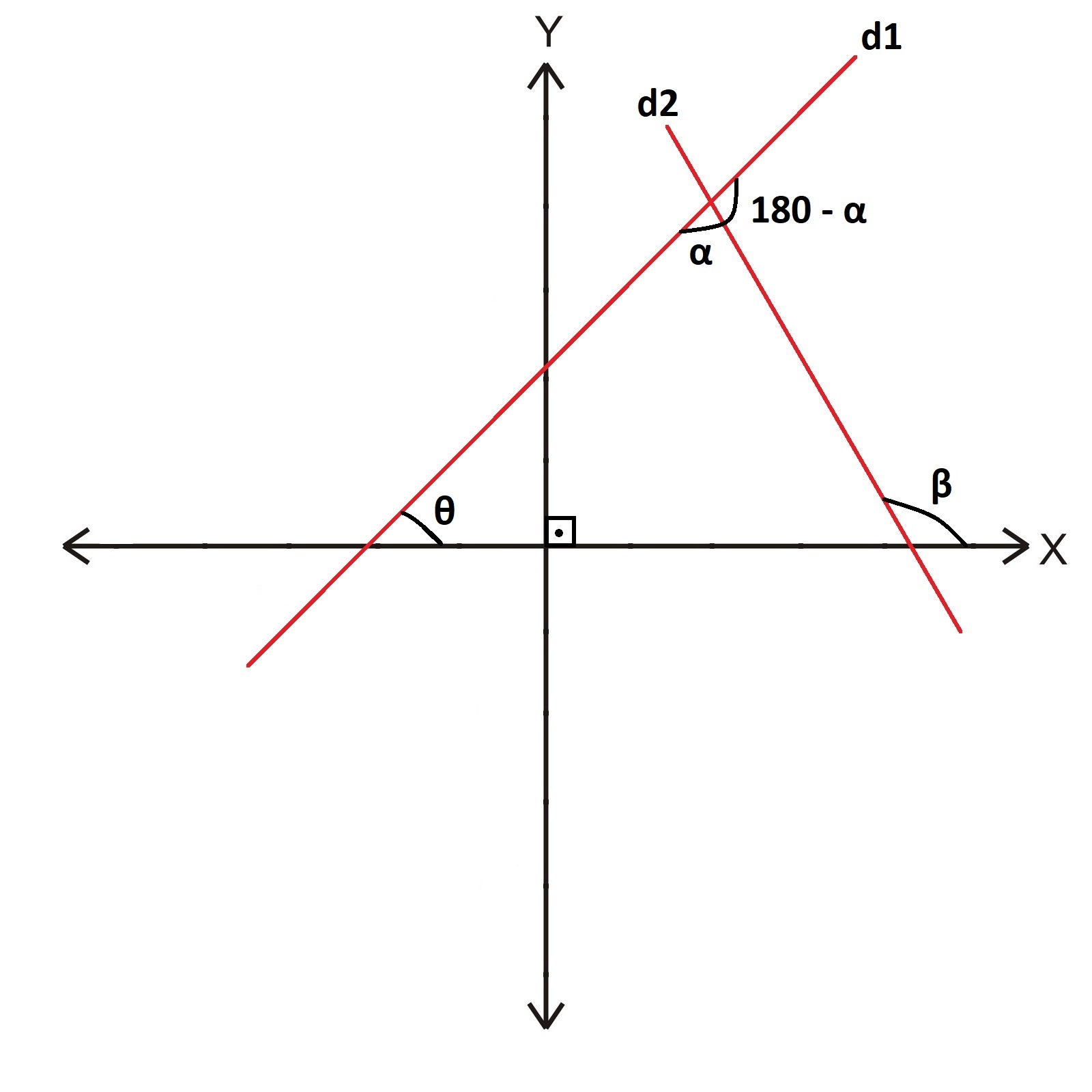
d1 doğrusunun eğimi, tanθ = m1
d2 doğrusunun eğimi, tanβ = m2
α = β – θ olmak üzere; 

\color{white}{tan\alpha = \frac{m_2 - m_1}{1 + m_1.m_2}}

Görüntüleme Sayısı: 12.675