Trigonometri – Konu Anlatımı (Özet)

Merkezi dik koordinat sisteminin başlangıç noktası 0 olan, yarıçap uzunluğu 1 birim olan çembere “Birim Çember” denir.

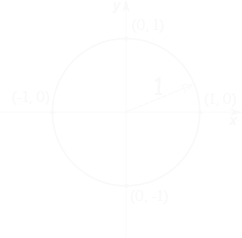
Trigonometrik Bağıntılar Ve Özellikleri:

A = \color{white}{\alpha.sinx \ + \ \beta.cosx} olmak üzere, A’nın alabileceği en büyük değer \color{white}{\sqrt{{\alpha}^2 + {\beta}^2}}  ve en küçük değer ise \color{white}{-\sqrt{{\alpha}^2 + {\beta}^2}} ‘dir.

Sinüs Teoremi: ABC üçgeninde çevresel çemberin yarıçapı R ve kenarları x, y, z olmak üzere;

Cosinüs Teoremi: ABC üçgenin kenarları a, b, c olmak üzere;

Açının 90 derece olması durumunda Cosinüs Teoreminden “Pisagor Bağıntısı” ortaya çıkar.

 

Toplam – Fark, Yarım Açı Formülleri:

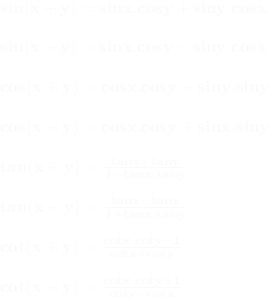
Ayrıca, tanjantın tersinin contanjanta eşit olduğuna dikkat edelim.

 

Trigonometrik Özdeşlikler:

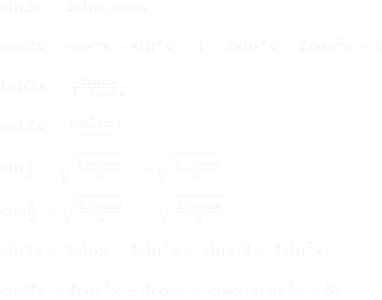
Bu formüllerin toplam-fark formüllerinden çıkarıldığını unutmayalım.

sin(-x) = -sinx,   cos(-x) = cosx,   tan(-x) = -tanx,   cot(-x) = -cotx  olup, cosinüs fonksiyonunun çift fonksiyon olduğuna dikkat edelim.

Dönüşüm Formülleri:

Ters Dönüşüm Formülleri:

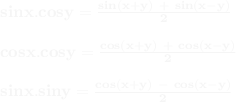
Periyodik Fonksiyon:

Ters Trigonometrik Fonksiyonlar:

arcsin [-1, 1] → [-π/2, π/2] arasında tanımlıdır.  \color{white}{arcsinx = sin^{-1}x} olarak gösterilir.

arccos [-1, 1] → [0, π] arasında tanımlıdır.  \color{white}{arccosx = cos^{-1}x} olarak gösterilir.

arctan R → (-π/2, π/2) arasında tanımlıdır.  \color{white}{arctanx = tan^{-1}x}  olarak gösterilir.

arccot R → (0, π) arasında tanımlıdır.  \color{white}{arccotx = cot^{-1}x} olarak gösterilir.

Trigonometrik Denklemler: 

0 ≤ a < 2π olmak üzere, sinx=sina için;
Çözüm Kümesi = {x|x1 =a + 2kπ  veya x2 = (180-a) + 2kπ, k ∈ Z}

0 ≤ a < 2π olmak üzere, cosx=cosa için;
Çözüm Kümesi = {x|x1 =a + 2kπ  veya x2 = -a + 2kπ, k ∈ Z}

0 ≤ a < π olmak üzere, tanx=tana için;
Çözüm Kümesi = {x|x = a + kπ , k ∈ Z}

0 ≤ a < π olmak üzere, cotx=cota için;
Çözüm Kümesi = {x|x = a + kπ , k ∈ Z}

Verilen aralıktaki değerleri çözüm kümesinde bulmak için k’ya değerler verilir.